MPQC  3.0.0-alpha
Object-Oriented Input

MPQC is an object-oriented program that directly allows the user to specify objects that MPQC then manipulates to obtain energies, properties, etc. This makes the input very flexible, but very complex. However, most calculations should be quite similar to the one of the examples given later in this chapter. The best way to get started is to use one of the example input files and modify it to meet your needs.

The object-oriented input format is described in the following sections:

Overview of the Object-Oriented Input

MPQC starts off by creating a ParsedKeyVal object that parses the input file specified on the command line. The format of the input file is documented in the KeyVal documentation(see The KeyVal Library). It is basically a free format input that associates keywords and logical groupings of keywords with values. The values can be scalars, arrays, or objects.

The keywords recognized by MPQC begin with the mpqc prefix. That is, they must be nested between an mpqc:( and a ). Alternately, each keyword can be individually prefixed by mpqc:. The primary keywords are given below. Some of the keywords specify objects, in which case the object will require more ParsedKeyVal input. These objects are created from the input by using their ParsedKeyVal constructors. These constructors are documented with the source code documentation for the class.

mole

This is the most important keyword for MPQC. It specifies the MolecularEnergy object. This is an object that knows how to compute the energy of a molecule. The specializations of MolecularEnergy that are most commonly used are CLKS, HSOSKS, UKS, CLHF, HSOSHF, UHF, and MBPT2.

opt

This keyword should be specified for geometry optimizations. It specifies an Optimize object. Usually, QNewtonOpt is best for finding minima and EFCOpt is best for transition states. See also optimize keyword.

optimize

The value of this keyword is boolean. If set to false then a geometry optimization will not be performed, whether opt was provided or not. If this keyword set to true, and opt was not provided, a geometry optimization will be performed with a default QNewtonOpt object (this is likely to be only useful for routinely finding minima on the potential surface). The default is true if a valid value for opt was provided, false otherwise.

grad

This keyword specifies the MolecularGradient object that will be used to compute nuclear forces, if they are necessary (i.e. if opt was given or do_grad was set to true. The only useful option at the moment is FinDispMolecularGradient. (see also the precise_findif option). This keyword will be ignored for mole objects that have analytic gradients implemented.

freq

This optional keyword will be checked in frequency computations (if do_freq=true). It specifies a MolecularFrequencies object. It may be necessary for testing purposes, i.e. for computing frequencies in lower point groups than used for computing mole. The default is to use a MolecularFrequency object initialized with mole's molecule object.

hess

This keyword specifies the MolecularHessian object that will be used to compute force constants. The only useful option at the moment is FinDispMolecularHessian. This keyword will be ignored for mole objects that have analytic hessians implemented.

freq_accuracy

This optional keyword will specify the relative accuracy with which the vibrational frequencies to be computed. This keyword is only used if do_freq=true. This specifies the target accuracy with which the hessian of mole will be computed. If the hessian is computed analytically, i.e. mole object supports analytic computation of the hessian, then this will be used if mole object does not have hessian_accuracy keyword. If the hessian is computed numerically and hess is given explicitly, this will be used if hess does not have accuracy keyword. The default is freq_accuracy=1e-5.

precise_findif

This boolean keyword specifies whether to compute FinDispMolecularGradient and/or FinDispMolecularHessian objects more accurately than normal. The default is false. If true, displacement size h will be set to 0.005 bohr, and contributions to the gradient/hessian quadratic in h will be eliminated, i.e. they will be accurate to the fourth power of h .

thread

This specifies an object of type ThreadGrp that can be used to advantage on shared-memory multiprocessor machines for certain types of calculations. This keyword can be overridden by giving the ThreadGrp in the environment or command line. See the section on running MPQC for more information.

integrals

This specifies an object of type Integral that will be used as the default integral evaluator. If MP2-R12 is used, then this should be set to use IntegralLibint2 with a line like integrals<IntegralLibint2>: ().

checkpoint

The value of this keyword is boolean. 

    <ul>

    <li><tt>true</tt> and optimization is to be performed <br />

    <tt>opt</tt> object will be checkpointed after each iteration.
    The checkpoint file suffix is ".ckpt".

    <li><tt>true</tt> and optimization is not performed <br />

    <tt>mole</tt> object will be checkpointed at intermediate points.
    The manner in which
    <tt>mole</tt> will be checkpointed depends on its particular type.
    The checkpoint file suffix is usually ".wfn", however
    in general it will depend on the particular specialization of
    <tt>MolecularEnergy</tt>.

    <li><tt>true</tt> and <tt>molgrad</tt> object is used to evaluate gradient
    numerically <br />

    <tt>molgrad</tt> object will be checkpointed after each displacement.
    The checkpoint file suffix is ".ckpt.grad".

    <li><tt>true</tt> and <tt>molhess</tt> object is used to evaluate hessian
    numerically <br />

    <tt>molhess</tt> object will be checkpointed after each displacement.
    The checkpoint file suffix is ".ckpt.hess".

    </ul>

    The default is to not checkpoint.
    </dd>

checkpoint_freq

This specifies how often to checkpoint certain MolecularEnergy specializations which compute iteratively. Currently, mole objects of SCF type can use this keyword. The default is 1, which means to checkpoint after every iteration.

savestate

The value of this keyword is boolean. If true, then the states of the Optimize and MolecularEnergy objects will be saved after the calculation completes. The output file suffixes are ".ckpt" and ".wfn", respectively. The default is to save state.

restart

The value of this keyword is boolean. If true, mpqc will attempt to restart the calculation. If the checkpoint file is not found, the calculation will continue as if the value were false. The default is true.

restart_file

This gives the name of a file from which restart information is read. If the file name ends with ".wfn" then MPQC will try to restore a MolecularEnergy object from it and query for the opt object in the input file. If the file name ends with ".ckpt" MPQC will try to restore an Optimize object from this file. The default file name is formed by appending ".ckpt" to the input file name with the extension removed.

do_energy

The value of this keyword is boolean. If true a single point energy calculation will be done for the MolecularEnergy object given with the mole keyword. The default is true.

do_gradient

The value of this keyword is boolean. If true and opt was not given then a single point gradient calculation will be done for the MolecularEnergy object given with the mole keyword. The default is false.

do_freq

The value of this keyword is boolean. If true a frequency calculation will be done for the MolecularEnergy object given with the mole keyword. If opt was also given then the frequency calculation will occur after a successful geometry optimization (in other words, if geometry optimization failed then the frequency computation will be skipped). The default is false.

write_pdb

The value of this keyword is boolean. If true a PDB file with the molecular coordinates will be written.

filename

The value of this keyword is a string that gives a name from which checkpoint and other filenames are constructed. The default is the basename of the input file.

print_timings

If this is true, timing information is printed at the end of the run. The default is true.

print_resources
If this is true, resources usage information is printed at the end of the run (
See also
ConsumableResources class). The default is true.
run

This gives a vector of objects of type Runnable. The run method for each of these objects will be called after the calculation completes. This can be used for computing properties, for example.

There are also some utility keywords that tell mpqc some technical details about how to do the calculation:

debug
This optional keyword gives a Debugger object which can be used to help find the problem if MPQC encounters a catastrophic error.
matrixkit
This optional keyword gives a SCMatrixKit specialization which is used to produce matrices of the desired type. The default is a ReplSCMatrixKit which replicates matrices on all of the nodes. Other choices are not thoroughly tested.

A Walk-Through of an Object-Oriented Input File

This example input does a Hartree-Fock calculation on water. Following is the entire input, followed by a breakdown with descriptions.

% This input does a Hartree-Fock calculation on water.
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
  )
)


We start with a descriptive comment. Comments begin with a %. Everything from the % to the end of the line is ignored.

% This input does a Hartree-Fock calculation on water.


Now lets set up a Molecule object. The name of the object comes first, it is molecule. Then, in angle brackets, comes the type of the molecule, which is the class Molecule. The keyword and class name are followed by a : and then several pieces of input grouped between a pair of matching parentheses. These parentheses contain the information that will be given to Molecule KeyVal constructor.

molecule<Molecule>: (


The point group of the molecule is needed. This is done by assigning symmetry to a case insensitive Schoenflies symbol that is used to initialize a PointGroup object. An Abelian point group should be used.

  symmetry = C2V


The default unit for the Cartesian coordinates is Bohr. You can specify other units by assigned unit to a string that will be used to initialize a Units object.

  unit = angstrom


Finally, the atoms and coordinates are given. This can be given in the shorthand table syntax shown below. The headings of the table are the keywords between the first pair of brackets. These are followed by an = and another pair of brackets that contain the data. The first datum is assigned to the first element of the array that corresponds to the first heading, atom. The second datum is assigned to the first element of the array associated with the second heading, geometry, and so on. Here the second datum is actually a vector: the x, y and z coordinates of the first atom.

  { atoms                       geometry                   } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)


Next, a basis set object is given.

basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)


Now we will give the main body of input. All the subsequent keywords will be grouped in the mpqc section of the input (that is, each keyword will be prefixed with mpqc:).

mpqc: (


Next we give the mole keyword which provides a specialization of the MolecularEnergy class. In this case we will do a closed-shell Hartree-Fock calculation. That is done with an object of type CLHF. The keywords that CLHF accepts are given with the documentation for the CLHF class, usually in the description of the const RefKeyVal& constructor for the class. Also with the CLHF documentation is a list of parent classes. Each of the parent classes may also have input. This input is included with the rest of the input for the child class.

  mole<CLHF>: (


The next line specifies the molecule to be used. There are two things to note, first that this is actually a reference to complete molecule specification elsewhere in the input file. The $ indicates that this is a reference and the keyword following the $ is the actual location of the molecule. The : in front of the keyword means that the keyword is not relative to the current location in the input, but rather relative to the root of the tree of keywords. Thus, this line grabs the molecule that was specified above. The molecule object could have been placed here, but frequently it is necessary that several objects refer to the exact same object and this can only be done using references.

The second point is that if you look at the documentation for CLHF, you will see that it doesn't read molecule keyword. However, if you follow its parent classes up to MolecularEnergy, you'll find that molecule is indeed read.

    molecule = $:molecule


Just as we gave molecule, specify the basis set with the basis keyword as follows:

    basis = $:basis


Now we close off the parentheses we opened above and we are finished.

  )
)


Sample Object-Oriented Input Files

The easiest way to get started with mpqc is to start with one of sample inputs that most nearly matches your problem. The src/bin/mpqc/samples contains all of the sample inputs below:

Hartree-Fock Energy

The following input will compute the Hartree-Fock energy of water.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
  )
)


MP2 Energy

The following input will compute the MP2 energy of water.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<MBPT2>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
    % reference wavefunction
    reference<CLHF>: (
      molecule = $:molecule
      basis = $:basis
      memory = 16000000
    )
  )
)


MP2-R12 energy

The following will compute the MP2-R12 energy of water in standard approximation A' (MP2-R12/A').

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "cc-pVDZ"
  molecule = $:molecule
)
% auxiliary basis set specification
abasis<GaussianBasisSet>: (
  name = "aug-cc-pVDZ"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<MBPT2_R12>: (
    molecule = $:molecule
    basis = $:basis
    aux_basis = $:abasis
    stdapprox = "A'"
    nfzc = 1
    memory = 16000000
    integrals<IntegralLibint2>:()
    % reference wavefunction
    reference<CLHF>: (
      molecule = $:molecule
      basis = $:basis
      memory = 16000000
      integrals<IntegralLibint2>:()
    )
  )
)


Hartree-Fock Optimization

The following input will optimize the geometry of water using the quasi-Newton method.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "6-31G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
  )
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Optimization

Some methods in MPQC cannot compute forces analytically. In this case it may be necessary to compute forces by finite diffrences. The following input will optimize the geometry of water using the quasi-Newton method with forces computed by finite differences of energies.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "6-31G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
  )
  % method for computing the molecule's energy
  mole<MBPT2>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
    nfzc = 1
    nfzv = 1
    method = zapt
    algorithm = v1
    reference<HSOSHF>: (
      multiplicity = 3
      molecule = $:molecule
      basis = $:basis
      memory = 16000000
    )
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
  % evaluate gradients by finite differences
  grad<FinDispMolecularGradient>: (
    energy = $..:mole
  )
)


Optimization with a Computed Guess Hessian

The following input will optimize the geometry of water using the quasi-Newton method. The guess Hessian will be computed at a lower level of theory.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "6-31G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
  )
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
    guess_hessian<FinDispMolecularHessian>: (
      molecule = $:molecule
      only_totally_symmetric = yes
      eliminate_quadratic_terms = no
      checkpoint = no
      energy<CLHF>: (
        molecule = $:molecule
        memory = 16000000
        basis<GaussianBasisSet>: (
          name = "3-21G"
          molecule = $:molecule
        )
      )
    )
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Optimization Using Newton's Method

The following input will optimize the geometry of water using the Newton's method. The Hessian will be computed at each step in the optimization. However, Hessian recomputation is usually not worth the cost; try using the computed Hessian as a guess Hessian for a quasi-Newton method before resorting to a Newton optimization.

% Emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = c2v
  unit = angstrom
  { atoms geometry } = {
     O     [     0.00000000     0.00000000     0.36937294 ]
     H     [     0.78397590     0.00000000    -0.18468647 ]
     H     [    -0.78397590     0.00000000    -0.18468647 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "3-21G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  restart = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
  )
  do_energy = no
  do_gradient = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
    coor = $..:coor
    guess_wavefunction<CLHF>: (
      molecule = $:molecule
      total_charge = 0
      basis<GaussianBasisSet>: (
        molecule = $:molecule
        name = "STO-3G"
      )
      memory = 16000000
    )
    hessian<FinDispMolecularHessian>: (
      only_totally_symmetric = yes
      eliminate_quadratic_terms = no
      checkpoint = no
    )
  )
  optimize = yes
  % optimizer object for the molecular geometry
  opt<NewtonOpt>: (
    print_hessian = yes
    max_iterations = 20
    function = $..:mole
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Hartree-Fock Frequencies

The following input will compute Hartree-Fock frequencies by finite displacements. A thermodynamic analysis will also be performed. If optimization input is also provided, then the optimization will be run first, then the frequencies.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C1
  { atoms geometry } = {
    O     [  0.0000000000    0.0000000000    0.8072934188 ]
    H     [  1.4325589285    0.0000000000   -0.3941980761 ]
    H     [ -1.4325589285    0.0000000000   -0.3941980761 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
  )
  do_freq = true
)


Giving Coordinates and a Guess Hessian

The following example shows several features that are really independent. The variable coordinates are explicitly given, rather than generated automatically. This is especially useful when a guess Hessian is to be provided, as it is here. This Hessian, as given by the user, is not complete and the QNewtonOpt object will fill in the missing values using a guess the Hessian provided by the MolecularEnergy object. Also, fixed coordinates are given in this sample input.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C1
  { atoms geometry } = {
      H    [ 0.088    2.006    1.438 ]
      O    [ 0.123    3.193    0.000 ]
      H    [ 0.088    2.006   -1.438 ]
      O    [ 4.502    5.955   -0.000 ]
      H    [ 2.917    4.963   -0.000 ]
      H    [ 3.812    7.691   -0.000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
  )
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
      extra_bonds = [ 2 5 ]
    )
    % use these instead of generated coordinates
    variable<SetIntCoor>: [
      <StreSimpleCo>:( atoms = [ 2 5 ] )
      <BendSimpleCo>:( atoms = [ 2 5 4 ] )
      <OutSimpleCo>: ( atoms = [ 5 2 1 3 ] )
      <SumIntCoor>: (
        coor: [
          <StreSimpleCo>:( atoms = [ 1 2 ] )
          <StreSimpleCo>:( atoms = [ 2 3 ] )
          ]
        coef = [ 1.0 1.0 ]
        )
      <SumIntCoor>: (
        coor: [
          <StreSimpleCo>:( atoms = [ 4 5 ] )
          <StreSimpleCo>:( atoms = [ 4 6 ] )
          ]
        coef = [ 1.0 1.0 ]
        )
      <BendSimpleCo>:( atoms = [ 1 2 3 ] )
      <BendSimpleCo>:( atoms = [ 5 4 6 ] )
    ]
    % these are fixed by symmetry anyway,
    fixed<SetIntCoor>: [
      <SumIntCoor>: (
        coor: [
          <StreSimpleCo>:( atoms = [ 1 2 ] )
          <StreSimpleCo>:( atoms = [ 2 3 ] )
          ]
        coef = [ 1.0 -1.0 ]
        )
      <SumIntCoor>: (
        coor: [
          <StreSimpleCo>:( atoms = [ 4 5 ] )
          <StreSimpleCo>:( atoms = [ 4 6 ] )
          ]
        coef = [ 1.0 -1.0 ]
        )
      <TorsSimpleCo>:( atoms = [ 2 5 4 6] )
      <OutSimpleCo>:( atoms = [ 3 2 6 4 ] )
      <OutSimpleCo>:( atoms = [ 1 2 6 4 ] )
    ]
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
    % give a partial guess hessian in internal coordinates
    % the missing elements will be filled in automatically
    hessian = [
        [  0.0109261670 ]
        [ -0.0004214845    0.0102746106  ]
        [ -0.0008600592    0.0030051330    0.0043149957 ]
        [  0.0             0.0             0.0          ]
        [  0.0             0.0             0.0          ]
        [  0.0             0.0             0.0          ]
        [  0.0             0.0             0.0          ]
     ]
  )
)


Optimization with a Hydrogen Bond

The automatic internal coordinate generator will fail if it cannot find enough redundant internal coordinates. In this case, the internal coordinate generator must be explicitly created in the input and given extra connectivity information, as is shown below.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C1
  { atoms geometry } = {
      H    [ 0.088    2.006    1.438 ]
      O    [ 0.123    3.193    0.000 ]
      H    [ 0.088    2.006   -1.438 ]
      O    [ 4.502    5.955   -0.000 ]
      H    [ 2.917    4.963   -0.000 ]
      H    [ 3.812    7.691   -0.000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
  )
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    % give an internal coordinate generator that knows about the
    % hydrogen bond between atoms 2 and 5
    generator<IntCoorGen>: (
      molecule = $:molecule
      extra_bonds = [ 2 5 ]
    )
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Fixed Coordinate Optimization

This example shows how to selectively fix internal coordinates in an optimization. Any number of linearly independent coordinates can be given. These coordinates must remain linearly independent throughout the optimization, a condition that might not hold since the coordinates can be nonlinear.

By default, the initial fixed coordinates' values are taken from the cartesian geometry given by the Molecule object; however, the molecule will be displaced to the internal coordinate values given with the fixed internal coordinates if have_fixed_values keyword is set to true, as shown in this example. In this case, the initial cartesian geometry should be reasonably close to the desired initial geometry and all of the variable coordinates will be frozen to their original values during the initial displacement.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = CS
  { atoms geometry } = {
    H [  3.04 -0.69 -1.59 ]
    H [  3.04 -0.69  1.59 ]
    N [  2.09 -0.48 -0.00 ]
    C [ -0.58 -0.15  0.00 ]
    H [ -1.17  1.82  0.00 ]
    H [ -1.41 -1.04 -1.64 ]
    H [ -1.41 -1.04  1.64 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "3-21G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
    have_fixed_values = yes
    fixed<SetIntCoor>: [
      <OutSimpleCo>: ( value = -0.1
                       label = "N-inversion"
                       atoms = [4 3 2 1] )
      ]
  )
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
  )
  % optimizer object for the molecular geometry
  opt<QNewtonOpt>: (
    max_iterations = 20
    function = $..:mole
    update<BFGSUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Transition State Optimization

This example shows a transition state optimization of the N-inversion in 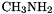$\mathrm{CH}_3\mathrm{NH}_2$ using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = CS
  { atoms geometry } = {
    H [  3.045436 -0.697438 -1.596748 ]
    H [  3.045436 -0.697438  1.596748 ]
    N [  2.098157 -0.482779 -0.000000 ]
    C [ -0.582616 -0.151798  0.000000 ]
    H [ -1.171620  1.822306  0.000000 ]
    H [ -1.417337 -1.042238 -1.647529 ]
    H [ -1.417337 -1.042238  1.647529 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "3-21G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
    followed<OutSimpleCo> = [ "N-inversion" 4 3 2 1 ]
  )  
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
  )
  % optimizer object for the molecular geometry
  opt<EFCOpt>: (
    transition_state = yes
    mode_following = yes
    max_iterations = 20
    function = $..:mole
    update<PowellUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Transition State Optimization with a Computed Guess Hessian

This example shows a transition state optimization of the N-inversion in 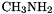$\mathrm{CH}_3\mathrm{NH}_2$ using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate. An approximate guess Hessian will be computed, which makes the optimiziation converge much faster in this case.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = CS
  { atoms geometry } = {
    H [  3.045436 -0.697438 -1.596748 ]
    H [  3.045436 -0.697438  1.596748 ]
    N [  2.098157 -0.482779 -0.000000 ]
    C [ -0.582616 -0.151798  0.000000 ]
    H [ -1.171620  1.822306  0.000000 ]
    H [ -1.417337 -1.042238 -1.647529 ]
    H [ -1.417337 -1.042238  1.647529 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "3-21G*"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = no
  % molecular coordinates for optimization
  coor<SymmMolecularCoor>: (
    molecule = $:molecule
    generator<IntCoorGen>: (
      molecule = $:molecule
    )
    followed<OutSimpleCo> = [ "N-inversion" 4 3 2 1 ]
  )  
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    coor = $..:coor
    memory = 16000000
    guess_hessian<FinDispMolecularHessian>: (
      molecule = $:molecule
      only_totally_symmetric = yes
      eliminate_quadratic_terms = no
      checkpoint = no
      energy<CLHF>: (
        molecule = $:molecule
        memory = 16000000
        basis<GaussianBasisSet>: (
          name = "3-21G"
          molecule = $:molecule
        )
      )
    )
  )
  % optimizer object for the molecular geometry
  opt<EFCOpt>: (
    transition_state = yes
    mode_following = yes
    max_iterations = 20
    function = $..:mole
    update<PowellUpdate>: ()
    convergence<MolEnergyConvergence>: (
      cartesian = yes
      energy = $..:..:mole
    )
  )
)


Hartree-Fock energy with intermediate checkpointing

The following two sections demonstrate how MPQC can be used to save the mole object periodically. This input will compute the Hartree-Fock energy of water while saving the mole object every 3 iterations.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = yes
  filename = "h2o-rhf-STO3G"
  checkpoint_freq = 3
  savestate = no
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
  )
)


The mole object will be saved to files named "h2o-rhf-STO3G.wfn.<iter#>.tmp" where <iter#> is the SCF iteration number (3, 6, etc.). Only the most recent file is kept, files from previous iterations are removed automatically. Keyword filename here is used to set the default file name prefix.

MP2-R12 energy with intermediate checkpointing

The following input will compute the MP2-R12 energy of water in standard approximation A' (MP2-R12/A') while saving the mole object at intermediate checkpoints.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "cc-pVDZ"
  molecule = $:molecule
)
% auxiliary basis set specification
abasis<GaussianBasisSet>: (
  name = "aug-cc-pVDZ"
  molecule = $:molecule
)
mpqc: (
  checkpoint = yes
  filename = "h2o-mp2r12ap-vdz-avdz"
  savestate = no
  % method for computing the molecule's energy
  mole<MBPT2_R12>: (
    molecule = $:molecule
    basis = $:basis
    aux_basis = $:abasis
    stdapprox = "A'"
    nfzc = 1
    memory = 16000000
    integrals<IntegralLibint2>:()
    % reference wavefunction
    reference<CLHF>: (
      molecule = $:molecule
      basis = $:basis
      memory = 16000000
      integrals<IntegralLibint2>:()
    )
  )
)


The mole object will be saved to a file named h2o-mp2r12ap-vdz-avdz.wfn". Keyword filename here is used to set the default file name prefix. Objects of the MBPT2_R12 type are checkpointed after the HF procedure, after the first integrals (SBS) transformation, and after the optional second (ABS) transformation.

HF gradient computed from a previously computed HF wave funtion

The following will illustrate how to reuse previously computed MolecularEnergy objects in subsequent computations. The first input computes Hartree-Fock energy for water and saves the mole object to file h2o-rhf-sto3g.wfn.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
mpqc: (
  checkpoint = no
  savestate = yes
  filename = "h2o-rhf-sto3g"
  % method for computing the molecule's energy
  mole<CLHF>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
  )
)


The second input reuses the mole object from the previous run to compute the gradient of the Hartree-Fock energy.

% emacs should use -*- KeyVal -*- mode
mpqc: (
  checkpoint = no
  savestate = no
  restart = yes
  restart_file = "h2o-rhf-sto3g.wfn"
  do_gradient = yes
)


MP2 Energy computed using precomputed Hartree-Fock wave function

The following input will compute the MP2 energy of water using a saved Hartree-Fock wave function obtained using the first input from HF gradient computed from a previously computed HF wave funtion.

% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
  symmetry = C2V
  unit = angstrom
  { atoms geometry } = {
    O     [     0.00000000     0.00000000     0.37000000 ]
    H     [     0.78000000     0.00000000    -0.18000000 ]
    H     [    -0.78000000     0.00000000    -0.18000000 ]
  }
)
% basis set specification
basis<GaussianBasisSet>: (
  name = "STO-3G"
  molecule = $:molecule
)
% wave function file object specification
wfnfile<BcastStateInBin>:file = "h2o-rhf-sto3g.wfn"
mpqc: (
  checkpoint = no
  savestate = no
  % method for computing the molecule's energy
  mole<MBPT2>: (
    molecule = $:molecule
    basis = $:basis
    memory = 16000000
    % reference wavefunction
    reference<SavableStateProxy>: (
      statein = $:wfnfile
      object = "CLHF"
    )
  )
)


Note that now object reference is of type SavableStateProxy, rather than CLHF. SavableStateProxy is a special object type that can be converted at runtime into the desired type (in this case, CLHF, as indicated by object).

Generated at Sun Jan 26 2020 23:24:02 for MPQC 3.0.0-alpha using the documentation package Doxygen 1.8.16.