Documentation

Permutation of a sequence of objects indexed by base-0 indices.

Warning: Unlike TiledArray::symmetry::Permutation, this fixes domain size.

Permutation class is used as an argument in all permutation operations on other objects. Permutations can be applied to sequences of objects:

b = p * a; // apply permutation p to sequence a and assign the result to

sequence b. a *= p; // apply permutation p (in-place) to sequence a.

Permutations can also be composed, e.g. multiplied and inverted:

p3 = p1 * p2; // computes product of permutations of p1 and p2

p1_inv = p1.inv(); // computes inverse of p1

Note

: Permutation is internally represented in one-line (image) form, e.g. $\left( \begin{tabular}{ccccc} 0 & 1 & 2 & 3 & 4 \\ 0 & 2 & 3 & 1 & 4 \end{tabular} \right)$ is represented in one-line form as $\{0, 2, 3, 1, 4\}$ . This means that 0th element of a sequence is mapped by this permutation into the 0th element of the permuted sequence (hence 0 is referred to as a fixed point of this permutation; so is 4); similarly, 1st element of a sequence is mapped by this permutation into the 2nd element of the permuted sequence (hence 2 is referred as the image of 1 under the action of this Permutation; similarly, 1 is the image of 3, etc.). Set $\{1, 2, 3\}$ is referred to as domain (or support) of this Permutation. Note that (by definition) Permutation maps its domain into itself (i.e. it's a bijection).

: Note that the one-line representation is redundant as multiple distinct one-line representations correspond to the same compressed form, e.g. $\{0, 2, 3, 1, 4\}$ and $\{0, 2, 3, 1\}$ correspond to the same $\{ 1 \to 2, 2 \to 3, 3 \to 1 \}$ compressed form. For an implementation using compressed form, and without fixed domain size, see TiledArray::symmetry::Permutation.

Definition at line 130 of file permutation.h.

Public Types
typedef Permutation	Permutation_

typedef unsigned int	index_type

template<typename T >
using	vector = container::svector< T >

typedef vector< index_type >::const_iterator	const_iterator

Public Member Functions
	Permutation ()=default

	Permutation (const Permutation &)=default

	Permutation (Permutation &&)=default

	~Permutation ()=default

Permutation &	operator= (const Permutation &)=default

Permutation &	operator= (Permutation &&other)=default

template<typename InIter , typename std::enable_if< detail::is_input_iterator< InIter >::value >::type * = nullptr>
	Permutation (InIter first, InIter last)
	Construct permutation from a range [first,last) More...

template<typename Index , typename = std::enable_if_t<detail::is_integral_range_v<Index>>>
	Permutation (const Index &a)
	Array constructor. More...

	Permutation (vector< index_type > &&a)
	std::vector move constructor More...

template<typename Integer , std::enable_if_t< std::is_integral_v< Integer >> * = nullptr>
	Permutation (std::initializer_list< Integer > list)
	Construct permutation with an initializer list. More...

index_type	size () const
	Domain size accessor. More...

index_type	dim () const
	Domain size accessor. More...

const_iterator	begin () const
	Begin element iterator factory function. More...

const_iterator	cbegin () const
	Begin element iterator factory function. More...

const_iterator	end () const
	End element iterator factory function. More...

const_iterator	cend () const
	End element iterator factory function. More...

index_type	operator[] (unsigned int i) const
	Element accessor. More...

vector< vector< index_type > >	cycles () const
	Cycles decomposition. More...

Permutation	identity () const
	Identity permutation factory function. More...

Permutation	mult (const Permutation &other) const
	Product of this permutation by `other`. More...

Permutation	inv () const
	Construct the inverse of this permutation. More...

Permutation	pow (int n) const
	Raise this permutation to the n-th power. More...

	operator bool () const
	Bool conversion. More...

bool	operator! () const
	Not operator. More...

const auto &	data () const
	Permutation data accessor. More...

template<typename Archive >
void	serialize (Archive &ar)
	Serialize permutation. More...

Static Public Member Functions
static Permutation	identity (const unsigned int dim)
	Identity permutation factory function. More...

Protected Attributes
vector< index_type >	p_
	One-line representation of permutation. More...

Member Typedef Documentation

◆ const_iterator

typedef vector<index_type>::const_iterator TiledArray::Permutation::const_iterator

Definition at line 136 of file permutation.h.

◆ index_type

typedef unsigned int TiledArray::Permutation::index_type

Definition at line 133 of file permutation.h.

◆ Permutation_

typedef Permutation TiledArray::Permutation::Permutation_

Definition at line 132 of file permutation.h.

◆ vector

template<typename T >

using TiledArray::Permutation::vector = container::svector<T>

Definition at line 135 of file permutation.h.

Constructor & Destructor Documentation

◆ Permutation() [1/7]

TiledArray::Permutation::Permutation ( )

default

◆ Permutation() [2/7]

TiledArray::Permutation::Permutation ( const Permutation & )

default

◆ Permutation() [3/7]

TiledArray::Permutation::Permutation ( Permutation && )

default

◆ ~Permutation()

TiledArray::Permutation::~Permutation ( )

default

◆ Permutation() [4/7]

template<typename InIter , typename std::enable_if< detail::is_input_iterator< InIter >::value >::type * = nullptr>

TiledArray::Permutation::Permutation	(	InIter	first,
		InIter	last
	)

inline

Construct permutation from a range [first,last)

Template Parameters

InIter An input iterator type

Parameters

first	The beginning of the iterator range
last	The end of the iterator range

Exceptions

TiledArray::Exception If the permutation contains any element that is greater than the size of the permutation or if there are any duplicate elements.

Definition at line 181 of file permutation.h.

◆ Permutation() [5/7]

template<typename Index , typename = std::enable_if_t<detail::is_integral_range_v<Index>>>

TiledArray::Permutation::Permutation ( const Index & a )

inlineexplicit

Array constructor.

Construct permutation from an Array

Parameters

a	The permutation array to be moved

Definition at line 191 of file permutation.h.

◆ Permutation() [6/7]

TiledArray::Permutation::Permutation ( vector< index_type > && a )

inlineexplicit

std::vector move constructor

Move the content of the vector into this permutation

Parameters

a	The permutation array to be moved

Definition at line 198 of file permutation.h.

◆ Permutation() [7/7]

template<typename Integer , std::enable_if_t< std::is_integral_v< Integer >> * = nullptr>

TiledArray::Permutation::Permutation ( std::initializer_list< Integer > list )

inlineexplicit

Construct permutation with an initializer list.

Template Parameters

Integer an integral type

Parameters

list	An initializer list of integers

Definition at line 208 of file permutation.h.

Member Function Documentation

◆ begin()

const_iterator TiledArray::Permutation::begin ( ) const

inline

Begin element iterator factory function.

Returns: An iterator that points to the beginning of the element range

Definition at line 226 of file permutation.h.

Here is the caller graph for this function:

◆ cbegin()

const_iterator TiledArray::Permutation::cbegin ( ) const

inline

Begin element iterator factory function.

Returns: An iterator that points to the beginning of the element range

Definition at line 231 of file permutation.h.

Here is the caller graph for this function:

◆ cend()

const_iterator TiledArray::Permutation::cend ( ) const

inline

End element iterator factory function.

Returns: An iterator that points to the end of the element range

Definition at line 241 of file permutation.h.

Here is the caller graph for this function:

◆ cycles()

vector<vector<index_type> > TiledArray::Permutation::cycles ( ) const

inline

Cycles decomposition.

Certain algorithms are more efficient with permutations represented as a set of cyclic transpositions. This function returns the set of cycles that represent this permutation. For example, permutation $\{3, 2, 1, 0 \}$ is represented as the following set of cycles: (0,3)(1,2). The canonical format for the cycles is:

Cycles of length 1 are skipped.
Each cycle is in order of increasing elements.
Cycles are in the order of increasing first elements.

Returns: the set of cycles (in canonical format) that represent this permutation

Definition at line 264 of file permutation.h.

◆ data()

const auto& TiledArray::Permutation::data ( ) const

inline

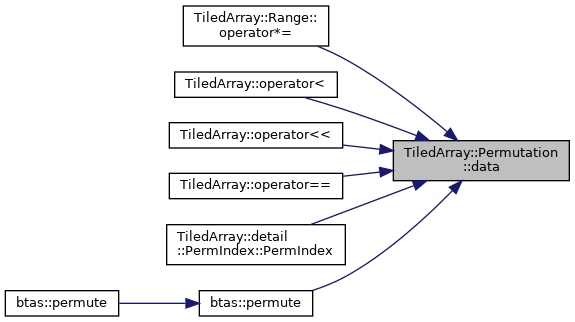
Permutation data accessor.

Returns: A reference to the array of permutation elements

Definition at line 388 of file permutation.h.

Here is the caller graph for this function:

◆ dim()

index_type TiledArray::Permutation::dim ( ) const

inline

Domain size accessor.

Returns: The domain size

Definition at line 219 of file permutation.h.

Here is the caller graph for this function:

◆ end()

const_iterator TiledArray::Permutation::end ( ) const

inline

End element iterator factory function.

Returns: An iterator that points to the end of the element range

Definition at line 236 of file permutation.h.

Here is the caller graph for this function:

◆ identity() [1/2]

Permutation TiledArray::Permutation::identity ( ) const

inline

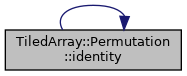
Identity permutation factory function.

Returns: An identity permutation

Definition at line 308 of file permutation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ identity() [2/2]

static Permutation TiledArray::Permutation::identity ( const unsigned int dim )

inlinestatic

Identity permutation factory function.

Parameters

dim	The number of dimensions in the

Returns: An identity permutation for dim elements

Definition at line 298 of file permutation.h.

Here is the call graph for this function:

◆ inv()

Permutation TiledArray::Permutation::inv ( ) const

inline

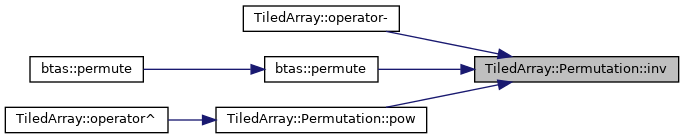
Construct the inverse of this permutation.

The inverse of the permutation is defined as $P \times P^{-1} = I$ , where $ I $ is the identity permutation.

Returns: The inverse of this permutation

Definition at line 334 of file permutation.h.

Here is the caller graph for this function:

◆ mult()

Permutation TiledArray::Permutation::mult ( const Permutation & other ) const

inline

Product of this permutation by other.

Parameters

other a Permutation

Returns: other * this, i.e. this applied first, then other

Definition at line 314 of file permutation.h.

Here is the caller graph for this function:

◆ operator bool()

TiledArray::Permutation::operator bool ( ) const

inlineexplicit

Bool conversion.

Returns: true if the permutation is not empty, otherwise false.

Definition at line 378 of file permutation.h.

◆ operator!()

bool TiledArray::Permutation::operator! ( ) const

inline

Not operator.

Returns: true if the permutation is empty, otherwise false.

Definition at line 383 of file permutation.h.

◆ operator=() [1/2]

Permutation& TiledArray::Permutation::operator= ( const Permutation & )

default

◆ operator=() [2/2]

Permutation& TiledArray::Permutation::operator= ( Permutation && other )

default

◆ operator[]()

index_type TiledArray::Permutation::operator[] ( unsigned int i ) const

inline

Element accessor.

Parameters

i	The element index

Returns: The i-th element

Definition at line 247 of file permutation.h.

◆ pow()

Permutation TiledArray::Permutation::pow ( int n ) const

inline

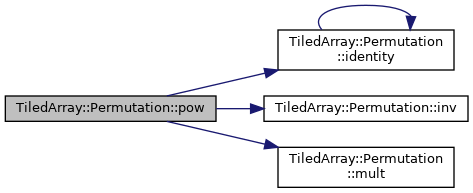
Raise this permutation to the n-th power.

Constructs the permutation $ P^n $ , where $ P $ is this permutation.

Parameters

n	Exponent value

Returns: This permutation raised to the n-th power

Definition at line 351 of file permutation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ serialize()

template<typename Archive >

void TiledArray::Permutation::serialize ( Archive & ar )

inline

Serialize permutation.

MADNESS compatible serialization function

Template Parameters

Archive The serialization archive type

Parameters

[in,out] ar The serialization archive

Definition at line 396 of file permutation.h.

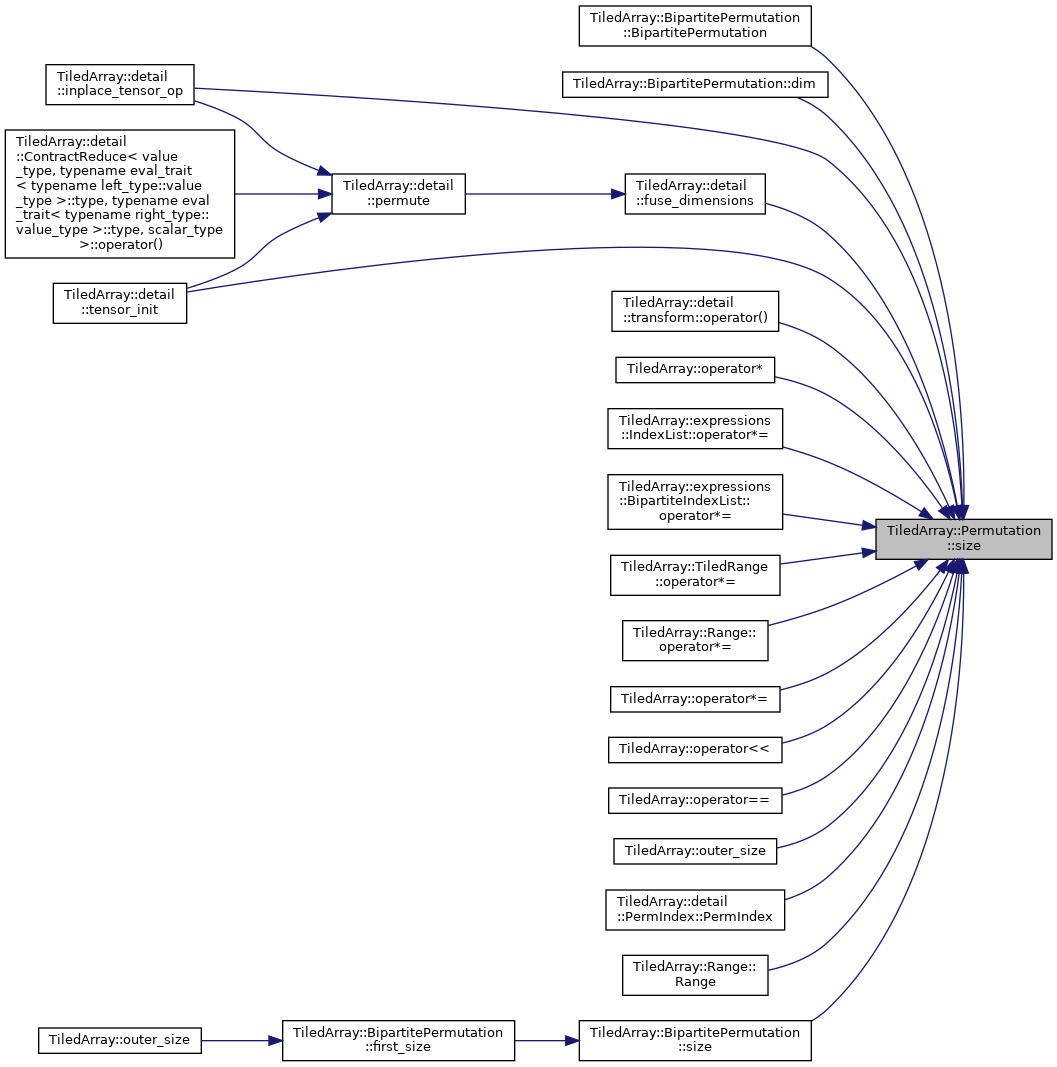
◆ size()

index_type TiledArray::Permutation::size ( ) const

inline

Domain size accessor.

Returns: The domain size

Definition at line 214 of file permutation.h.

Here is the caller graph for this function:

Member Data Documentation

◆ p_

vector<index_type> TiledArray::Permutation::p_

protected

One-line representation of permutation.

Definition at line 161 of file permutation.h.

The documentation for this class was generated from the following file:

TiledArray/permutation.h

Documentation

Public Types

Public Member Functions

Static Public Member Functions

Protected Attributes

Member Typedef Documentation

◆ const_iterator

◆ index_type

◆ Permutation_

◆ vector

Constructor & Destructor Documentation

◆ Permutation() [1/7]

◆ Permutation() [2/7]

◆ Permutation() [3/7]

◆ ~Permutation()

◆ Permutation() [4/7]

◆ Permutation() [5/7]

◆ Permutation() [6/7]

◆ Permutation() [7/7]

Member Function Documentation

◆ begin()

◆ cbegin()

◆ cend()

◆ cycles()

◆ data()

◆ dim()

◆ end()

◆ identity() [1/2]

◆ identity() [2/2]

◆ inv()

◆ mult()

◆ operator bool()

◆ operator!()

◆ operator=() [1/2]

◆ operator=() [2/2]

◆ operator[]()

◆ pow()

◆ serialize()

◆ size()

Member Data Documentation

◆ p_