Documentation
Permutation of a sequence of objects indexed by base-0 indices.
- Warning
- Unlike TiledArray::Permutation, this does not fix domain size.
Permutation class is used as an argument in all permutation operations on other objects. Permutations can be applied to sequences of objects:
Permutations can also be composed, e.g. multiplied and inverted:
- Note
- Unlike TiledArray::Permutation, which is internally represented in one-line form, TiledArray::symmetry::Permutation is internally represented in compressed two-line form. E.g. the following permutation in Cauchy's two-line form,
 , is represented in compressed form as
, is represented in compressed form as  . This means that 0th element of a sequence is mapped by this permutation into the 0th element of the permuted sequence (hence 0 is referred to as a fixed point of this permutation; so is 4); similarly, 1st element of a sequence is mapped by this permutation into the 2nd element of the permuted sequence (hence 2 is referred as the image of 1 under the action of this Permutation; similarly, 1 is the image of 3, etc.). Set
. This means that 0th element of a sequence is mapped by this permutation into the 0th element of the permuted sequence (hence 0 is referred to as a fixed point of this permutation; so is 4); similarly, 1st element of a sequence is mapped by this permutation into the 2nd element of the permuted sequence (hence 2 is referred as the image of 1 under the action of this Permutation; similarly, 1 is the image of 3, etc.). Set  is referred to as domain (or support) of this Permutation. Note that (by definition) Permutation maps its domain into itself (i.e. it's a bijection).
is referred to as domain (or support) of this Permutation. Note that (by definition) Permutation maps its domain into itself (i.e. it's a bijection).
- As a reminder, permutation
 is represented in one-line form as
is represented in one-line form as  . Note that the one-line representation is redundant as multiple distinct one-line representations correspond to the same compressed form, e.g.
. Note that the one-line representation is redundant as multiple distinct one-line representations correspond to the same compressed form, e.g.  and
and  correspond to the same
correspond to the same  compressed form.
compressed form.
- Another non-redundant representation of Permutation is as a set of cycles. For example, permutation
 is represented uniquely as the following set of cycles: (0,3)(1,2). The canonical format for the cycle decomposition used by Permutation class is defined as follows:
is represented uniquely as the following set of cycles: (0,3)(1,2). The canonical format for the cycle decomposition used by Permutation class is defined as follows: - Cycles of length 1 are skipped.
- Each cycle is in order of increasing elements.
- Cycles are in the order of increasing first elements.
Definition at line 117 of file permutation.h.
Public Types | |
| typedef Permutation | Permutation_ |
| typedef unsigned int | index_type |
| template<typename T > | |
| using | vector = container::svector< T > |
| typedef std::map< index_type, index_type > | Map |
| typedef Map::const_iterator | const_iterator |
Public Member Functions | |
| Permutation ()=default | |
| Permutation (const Permutation &)=default | |
| Permutation (Permutation &&)=default | |
| ~Permutation ()=default | |
| Permutation & | operator= (const Permutation &)=default |
| Permutation & | operator= (Permutation &&other)=default |
| template<typename InIter , typename std::enable_if< TiledArray::detail::is_input_iterator< InIter >::value >::type * = nullptr> | |
| Permutation (InIter first, InIter last) | |
| Construct permutation using its 1-line form given by range [first,last) More... | |
| template<typename Index , typename std::enable_if< TiledArray::detail::is_integral_range_v< Index >, bool >::type * = nullptr> | |
| Permutation (Index &&a) | |
| Construct permutation using 1-line form given as an integral range. More... | |
| template<typename Integer , std::enable_if_t< std::is_integral_v< Integer >> * = nullptr> | |
| Permutation (std::initializer_list< Integer > list) | |
| Construct permutation with an initializer list. More... | |
| Permutation (Map p) | |
| Construct permutation using its compressed 2-line form given by std::map. More... | |
| unsigned int | domain_size () const |
| Permutation domain size. More... | |
| index_type | operator[] (index_type e) const |
| Computes image of an element under this permutation. More... | |
| template<typename Set > | |
| Set | domain () const |
| Computes the domain of this permutation. More... | |
| template<typename Integer , typename std::enable_if< std::is_integral< Integer >::value >::type * = nullptr> | |
| bool | is_in_domain (Integer i) const |
| Test if an index is in the domain of this permutation. More... | |
| vector< vector< index_type > > | cycles () const |
| Cycles decomposition. More... | |
| Permutation | mult (const Permutation &other) const |
Product of this permutation by other. More... | |
| Permutation | inv () const |
| Construct the inverse of this permutation. More... | |
| Permutation | pow (int n) const |
| Raise this permutation to the n-th power. More... | |
| const Map & | data () const |
| Data accessor. More... | |
| Permutation | identity () const |
| Idenity permutation factory method. More... | |
| template<typename Archive > | |
| void | serialize (Archive &ar) |
| Serialize permutation. More... | |
Iterator accessors | |
Permutation iterators dereference into | |
| const_iterator | begin () const |
| Begin element iterator factory function. More... | |
| const_iterator | cbegin () const |
| Begin element iterator factory function. More... | |
| const_iterator | end () const |
| End element iterator factory function. More... | |
| const_iterator | cend () const |
| End element iterator factory function. More... | |
Friends | |
| std::ostream & | operator<< (std::ostream &output, const Permutation &p) |
| Add permutation to an output stream. More... | |
Member Typedef Documentation
◆ const_iterator
| typedef Map::const_iterator TiledArray::symmetry::Permutation::const_iterator |
Definition at line 124 of file permutation.h.
◆ index_type
| typedef unsigned int TiledArray::symmetry::Permutation::index_type |
Definition at line 120 of file permutation.h.
◆ Map
| typedef std::map<index_type, index_type> TiledArray::symmetry::Permutation::Map |
Definition at line 123 of file permutation.h.
◆ Permutation_
Definition at line 119 of file permutation.h.
◆ vector
| using TiledArray::symmetry::Permutation::vector = container::svector<T> |
Definition at line 122 of file permutation.h.
Constructor & Destructor Documentation
◆ Permutation() [1/7]
|
default |
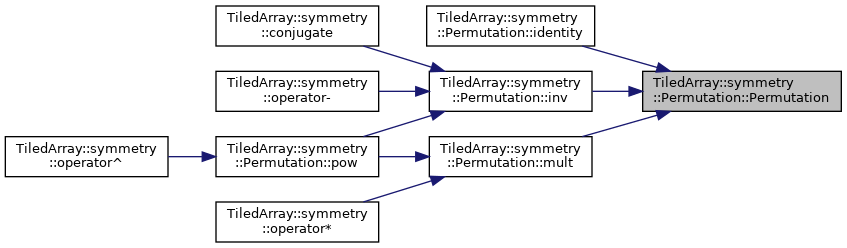
◆ Permutation() [2/7]
|
default |
◆ Permutation() [3/7]
|
default |
◆ ~Permutation()
|
default |
◆ Permutation() [4/7]
|
inline |
Construct permutation using its 1-line form given by range [first,last)
- Template Parameters
-
InIter An input iterator type
- Parameters
-
first The beginning of the iterator range last The end of the iterator range
- Exceptions
-
TiledArray::Exception if invalid input is given.
- See also
- valid_permutation(first,last)
Definition at line 200 of file permutation.h.
◆ Permutation() [5/7]
|
inlineexplicit |
Construct permutation using 1-line form given as an integral range.
- Template Parameters
-
Index An integral range type
- Parameters
-
a range that specifies permutation in 1-line form
Definition at line 216 of file permutation.h.
◆ Permutation() [6/7]
|
inlineexplicit |
Construct permutation with an initializer list.
- Template Parameters
-
Integer an integral type
- Parameters
-
list An initializer list of integers
Definition at line 224 of file permutation.h.
◆ Permutation() [7/7]
|
inline |
Construct permutation using its compressed 2-line form given by std::map.
- Parameters
-
p the map
Definition at line 230 of file permutation.h.
Member Function Documentation
◆ begin()
|
inline |
Begin element iterator factory function.
- Returns
- An iterator that points to the beginning of the range
Definition at line 249 of file permutation.h.
◆ cbegin()
|
inline |
Begin element iterator factory function.
- Returns
- An iterator that points to the beginning of the range
Definition at line 254 of file permutation.h.
◆ cend()
|
inline |
End element iterator factory function.
- Returns
- An iterator that points to the end of the range
Definition at line 264 of file permutation.h.
◆ cycles()
|
inline |
Cycles decomposition.
Certain algorithms are more efficient with permutations represented as a set of cyclic transpositions. This function returns the set of cycles that represent this permutation. For example, permutation  is represented as the following set of cycles: (0,3)(1,2). The canonical format for the cycles is:
is represented as the following set of cycles: (0,3)(1,2). The canonical format for the cycles is:
- Cycles of length 1 are skipped.
- Each cycle is in order of increasing elements.
- Cycles are in the order of increasing first elements.
- Returns
- the set of cycles (in canonical format) that represent this permutation
Definition at line 320 of file permutation.h.
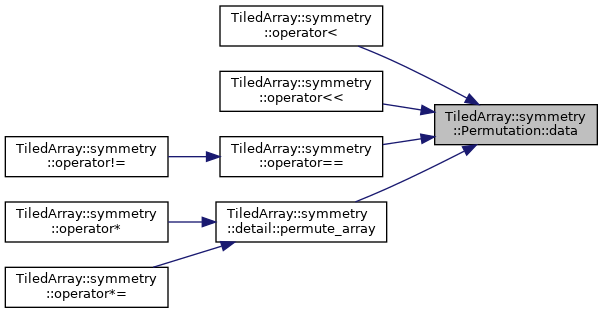
◆ data()
|
inline |
Data accessor.
gives direct access to std::map that encodes the Permutation
- Returns
std::map<index_type,index_type>object encoding the permutation in compressed two-line form
Definition at line 425 of file permutation.h.
◆ domain()
|
inline |
Computes the domain of this permutation.
- Template Parameters
-
Set a container type in which the result will be returned
- Returns
- the domain of this permutation, as a Set
Definition at line 286 of file permutation.h.

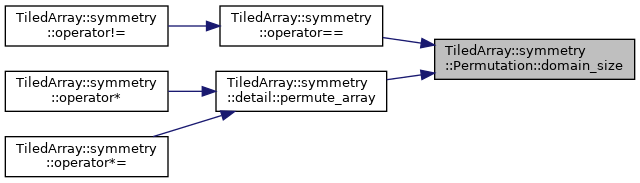
◆ domain_size()
|
inline |
Permutation domain size.
- Returns
- The number of elements in the domain of permutation
Definition at line 235 of file permutation.h.
◆ end()
|
inline |
End element iterator factory function.
- Returns
- An iterator that points to the end of the range
Definition at line 259 of file permutation.h.
◆ identity()
|
inline |
Idenity permutation factory method.
- Returns
- the identity permutation
Definition at line 430 of file permutation.h.

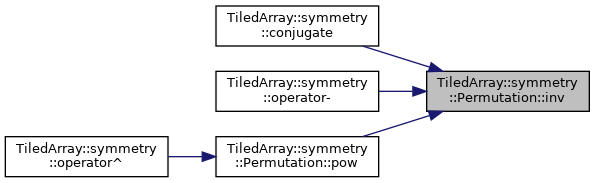
◆ inv()
|
inline |
Construct the inverse of this permutation.
The inverse of permutation  is defined as
is defined as  , where
, where  is the identity permutation.
is the identity permutation.
- Returns
- The inverse of this permutation
Definition at line 381 of file permutation.h.

◆ is_in_domain()
|
inline |
Test if an index is in the domain of this permutation.
- Template Parameters
-
Integer an integer type
- Parameters
-
i an index whose presence in domain is tested
- Returns
true, ifiis in the domain,falseotherwise
Definition at line 303 of file permutation.h.
◆ mult()
|
inline |
Product of this permutation by other.
- Parameters
-
other a Permutation
- Returns
other*this, i.e.thisapplied first, thenother
Definition at line 360 of file permutation.h.

◆ operator=() [1/2]
|
default |
◆ operator=() [2/2]
|
default |
◆ operator[]()
|
inline |
Computes image of an element under this permutation.
- Parameters
-
e input index
- Returns
- the image of element
e; ifeis in the domain of this permutation, returns its image, otherwise returnse
Definition at line 273 of file permutation.h.
◆ pow()
|
inline |
Raise this permutation to the n-th power.
Constructs the permutation  , where
, where  is this permutation.
is this permutation.
- Parameters
-
n Exponent value
- Returns
- This permutation raised to the n-th power
Definition at line 397 of file permutation.h.


◆ serialize()
|
inline |
Serialize permutation.
MADNESS compatible serialization function
- Template Parameters
-
Archive The serialization archive type
- Parameters
-
[in,out] ar The serialization archive
Definition at line 438 of file permutation.h.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Add permutation to an output stream.
- Parameters
-
[out] output The output stream [in] p The permutation to be added to the output stream
- Returns
- The output stream
Definition at line 481 of file permutation.h.
The documentation for this class was generated from the following file:
- TiledArray/symm/permutation.h
 dereferences to
dereferences to  1.8.20
1.8.20