TiledArray is a framework for computing with block-sparse tensors on shared- and distributed-memory computers. It is designed to allow users to compose tensor expressions of arbitrary complexity in native C++ code that closely resembles the standard mathematical notation. TiledArray is designed for strong scalability in real applications, with pilot benchmarks having executed on hundreds of thousands of cores.

TiledArray is built on top of the MADNESS parallel runtime, denoted here as MADWorld. MADWorld provides a powerful task-based programming model that is key to TiledArray's scalability.

This document is intended for new users of TiledArray. It covers basic concepts, construction and initialization of tensors, composing tensor expressions, and accessing results. More advanced users are directed elsewhere in this Wiki for topics such as user-defined Tiles, etc.

NOTE: This guide, and TiledArray itself, is a work in progress. Therefore information may be changed or added at any time. While we strive to maintain a stable user interface, TiledArray is still evolving, sometimes in non-backward-compatible ways.

Primer

Concepts

Tensor/Array

TiledArray represents tensors as ordinary (multidimensional) arrays of values (i.e. nothing specifies the transformation properties of the array data to make it a proper tensor); henceforth we will use tensor and array interchangeably. An order-_n_ tensor (i.e., a tensor with n indices) is represented as an n-dimensional array. Tensor in TiledArray is a map from a Range of Indices (a hyperrectangular range in ℤⁿ) to ring ℜ. The highest-level tensor data structure in TiledArray is a distributed tiled multidimensional array, modeling concept DistArray and represented by C++ class DistArray. DistArray is a directly-addressable sequence of tiles. Tiles are distributed among all or some processes in your application, hence only a subset of tiles is rapidly accessible from a given process. A DistArray is defined by a TiledRange, which specifies a cartesian tiling of the element Range, a Pmap, which maps tile index to the processor on which it resides, and a Shape, which specifies the structure of the array at the tile level (e.g. it can indicate whether a given tile is zero or not in a sparse array). TiledArray supports two variants of DistArray out of the box: dense, in which all tiles are assumed non-zero, and block-sparse, in which some tiles may be assumed to be zero, and thus omitted.

Range

An order-_n_ Range is a hyperrectangle in ℤⁿ, where n ≥ 0 (currently TiledArray only supports ranges in the nonnegative subset of ℤⁿ). Range is used to define valid values for element and tile Indices. The size of each mode (side) of the hyperrectangle is its extent; 0-based indexing of modes is used throughout.

Index

Index specifies a location in a range. An index may be a coordinate index or an ordinal index.

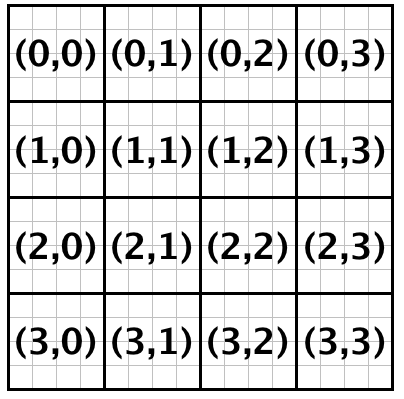
Coordinate Index

A sequence of non-negative n integers that represents an element of a Range. The first integer refers to the 0th mode of the range, etc. The following figure illustrates coordinate indices of the elements of a 4 by 4 matrix.

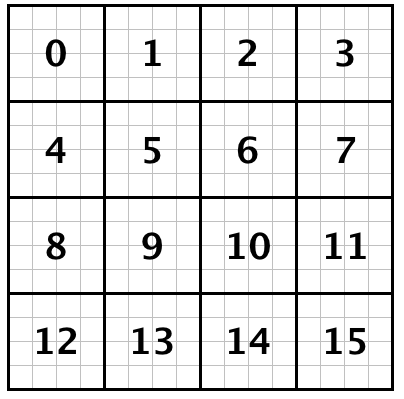
Ordinal Index

A single nonnegative integer value specifying the position of an element in a totally-ordered Range. Row-major lexicographical order is used by most classes in TiledArray. The following figure illustrates (row-major) ordinal indices of the elements of a 4 by 4 matrix.

TiledRange

TiledRange is a Range each mode of which is tiled, i.e. divided into contiguous, non-overlaping blocks; cartesian product of mode tilings defines the overall tiling of the range into subranges; each such subrange is a tile of the TiledRange. Tiles in a TiledRange are indexed just like the elements of the underlying range, hence the notions of element range and tile range arise in discussing TiledRange .

Tile

Tile of an array is any hyperrectangular sub-block of the array; a Tile is an array of same order as the base array. Division of DistArray into tiles is defined by its TiledRange. Tiles are local objects, i.e. only the process on which the tile resides has access to its data. Tile is defined by its Range.

Dense Array

A dense array is an array where all tiles are explicitly stored. All tiles of a dense array are non-zero tiles.

Block-Sparse Array

In a block-spare array, only non-zero blocks are stored. For example, the array pictured below contains four non-zero blocks (shown in green). You may specify any block in an array to be a zero tile or non-zero tile. For example, a 2D, block-sparse array may look like:

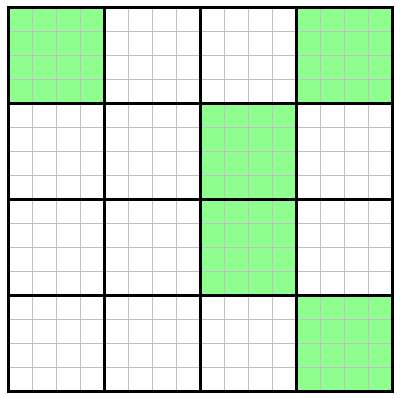
where zero tiles are shown in white, while non-zero tiles are shown in green.

Non-Zero and Zero Tiles

A non-zero tile is a sub-block of a DistArray that explicitly stores all elements for that tile. A zero tile is a sub-block of a DistArray that implicitly contains all zero elements, but is never stored. where all elements are equal to zero (Note: The data for zero tiles is not explicitly stored).

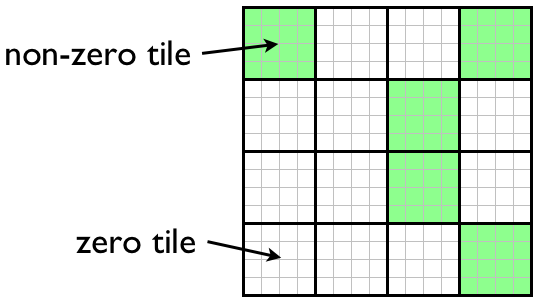
Owner

The owner of a tile is the process which stores that tile.

Pmap

A process map that defines ownership of each tile.

Shape

An object that specifies the structure of DistArray. E.g. it could be represented by a bitset where a set bit represents a non-zero tile and an unset bit represents zero tiles in a DistArray.

Implementation

TiledArray is a library written in standard C++ using features available in the 2017 ISO standard (commonly known as C++17). To use TiledArray it is necessary to #include header tiledarray.h. imports most TiledArray features into namespace TiledArray. For convenience, namespace alias TA is also provided. Although the alias can be disabled by defining the TILEDARRAY_DISABLE_NAMESPACE_TA preprocessor variable, all examples will assume that the TA alias is not disabled.

P.S. It sometimes may be possible to reduce source code couplings by importing only forwarding declarations. This is done by #includeing header tiledarray_fwd.h.

Parallel Runtime

TiledArray exposes several features of the MADWorld programming model, most importantly worlds, tasks, and futures.

A world, represented by an object of TA::World class (which is currently just an alias to madness::World), represents a collection of MPI processes. World is an extension of the MPI (intra)communicator concept that provides not only a communication context but also an execution context (such as task queue, etc.). Each array in TiledArray lives in a specific world (the default world, just like MPI_COMM_WORLD, spans the entire set of processes which called MPI_Init_thread).

Task is a unit of execution in MADWorld. Most operations in TiledArray are expressed as a collection of fine-grained tasks scheduled by the MADWorld; the fine-grained nature of tasks allows to express much more parallelism than is possible with traditional approaches like fork-join. Task parallel runtime of MADWorld also allows to overlap task execution (computation) with data movement (communication), and thus tolerate better all sources of latency.

When submitting a task to the task queue, a madness::Future object is returned, which is a placeholder for the result of a task. Futures may also be given to other tasks as input. In this way, futures are used to define task dependencies; they can be thought as nodes of the graph of tasks representing the computation. Note that MADWorld futures are similar to std::future (or, rather, std::shared_future) in standard C++, the main distinction is that madness::Future is global (i.e. a Future on one process can refer to a result produced on another) and it is possible to attach continuations to madness::Future.

Using TiledArray

A typical scenario for using TiledArray will perform the following steps:

Initialize the parallel runtime environment
Construct DistArray objects
Initialize tile data of the arrays
Implement algebraic tensor expressions Let's walk through each step in detail.

Initializing the Parallel Runtime Environment

To use TiledArray it is necessary to first initialize its runtime environment, such as MADNESS and its dependents, CUDA, etc:

#include <tiledarray.h> // imports most TiledArray features
 
int main(int argc, char* argv[]) {
  // Initialize TiledArray
  auto& world = TA::initialize(argc, argv);
 
  // Do some work here.
 
  TA::finalize();
  return 0;
}

TA::initialize initializes the TiledArray runtime and returns a reference to the default World object, which by default spans all MPI processes. TA::finalize shuts down the TiledArray runtime; after this it is no longer possible to use TiledArray, so this is typically done at the very end of the program. It is not possible to call TA::initialize more than once in your program.

Since TiledArray depends on MPI (via MADWorld), TA::initialize first checks if MPI had been initialized. If MPI is not yet initialized TA::initialize will do so by calling MPI_Init_thread. If MPI had already been initialized, then TA::initialize will only check that MPI initialization requested proper level of thread safety (serialized or full).

It is easy to initialize TiledArray on a subset of MPI processes by passing the corresponding MPI communicator to TA::initialize:

#include <tiledarray.h>
 
int main(int argc, char* argv[]) {
  // Initialize MPI
  int thread_level_provided;
  MPI_Init_thread(&argc, &argv, MPI_THREAD_MULTIPLE, &thread_level_provided);
  assert(MPI_THREAD_MULTIPLE == thread_level_provided);
 
  // create a communicator spanning even ranks only
  int me;  MPI_Comm_rank(MPI_COMM_WORLD, &me);
  MPI_Comm comm_evens; MPI_Comm_split(MPI_COMM_WORLD, (me % 2 ? MPI_UNDEFINED : 0), 0, &comm_evens);
 
  // Initialize TiledArray on even ranks only
  if (comm_evens != MPI_COMM_NULL) {
    auto& world = TA::initialize(argc, argv, comm_evens);
 
    // Do some work here.
 
    // Finalize TiledArray
    TA::finalize();
  }
 
  // must finalize MPI since we initialized it ourselves
  MPI_Finalize();
 
  return 0;
}

Construct an array

To construct a DistArray object, you must supply following the meta data:

TiledRange
(optional) Pmap
(block-sparse only) Shape

Construct TiledRange object

A TiledRange is defined by tensor/Cartesian product of tilings for each mode. Tiling for 1 mode is represented by class TA::TiledRange1 which is most easily constructed by specifying tile boundaries as an array of indices. For example, the following code defines 2 tilings for interval [0,10), both consisting of 3 tiles:

TA::TiledRange1 TR0{0,3,8,10};

TA::TiledRange1 TR1{0,4,7,10};

The size of tiles in TR0 are 3, 5, and 2, whereas TR1's tiles has sizes 4, 3, and 3. Combining these tilings produces an order-2 TiledRange,

TA::TiledRange TR{TR0,TR1};

with 3 tiles in each mode, for a total of 10 x 10 (or 100) elements partitioned into 9 tiles, as pictured below:

[[images/tiledrange.png|height=250px]]

TR can be constructed directly without defining TiledRange1 objects first as follows:

TA::TiledRange TR{{0,3,8,10},

{0,4,7,10}};

The TiledRange constructor in the above example is useful for simple examples and prototyping code. However, in production code it will be likely necessary to construct TiledRange objects with an iterator list of TiledRange1 objects, e.g.:

// Construct tile boundary vector
std::vector<std::size_t> tile_boundaries;
for(std::size_t i = 0; i <= 16; i += 4)
  tile_boundaries.push_back(i);
 
// Construct a set of 1D TiledRanges
std::vector<TA::TiledRange1>
    ranges(2, TA::TiledRange1(tile_boundaries.begin(), tile_boundaries.end()));
 
// Construct the 2D TiledRange
TA::TiledRange trange(ranges.begin(), ranges.end());

where tile_boundaries defines the boundaries of tiles along a single dimension, ranges is the set of tile boundaries (one per dimension), and trange is the tiled range object that is used to construct DistArray objects.

Construct a Process Map Object

A process map is used to determine owner of a given tile with requiring communication between processes. Process maps also maintain a list of local tiles (tiles owned by the current process). TiledArray provides several different types process maps that can be used to initialize DistArray objects. The process maps provided by TiledArray are blocked, block-cyclic, hashed, and replicated. With the exception of the replicated process map (which always returns the current process as the owner) a process map will always return the same owner for a given tile on any process. You may also create a custom process map class that is derived from TA::Pmap.

Note: You are not required to explicitly construct a process map for a DistArray object as the DistArray object will construct one for you if none is provided. You may want to construct a process map yourself if you require a particular data layout. Process maps can also be used aid in the distribution of work among processes before your array object is constructed (this may be useful when constructing sparse shapes).

To construct a process map using one of the process map provided by TiledArray:

const std::size_t m = 20;
const std::size_t n = 10;
 
std::shared_ptr<TA::Pmap>
    blocked_pmap(new TA::detail::BlockedPmap(world, m * n));
 
// {4,4} = # of processor rows/columns in 2d grid ... hardwired here, but should be determined programmatically
std::shared_ptr<TA::Pmap>
    cyclic_pmap(new TA::detail::CyclicPmap(world, m, n, 4, 4));
 
std::shared_ptr<TA::Pmap>
    hash_pmap(new TA::detail::HashPmap(world, m * n));

An program is provided by TiledArray in examples/pmap_test/ that demonstrates the tile distribution that is generated by the various process map objects. You can vary the output of this program by changing the number of MPI processes when running the test program. For example, the output for 16 MPI processes looks like:

$ mpirun -n 16 pmap
MADNESS runtime initialized with 7 threads in the pool and affinity -1 -1 -1
Block
0  0  0  0  0  0  0  0  0
0  0  1  1  1  1  1  1  1
1  1  1  1  1  2  2  2  2
2  2  2  2  2  2  2  2  3
3  3  3  3  3  3  3  3  3
3  4  4  4  4  4  4  4  4
4  4  4  4  5  5  5  5  5
5  5  5  5  5  5  5  6  6
6  6  6  6  6  6  6  6  6
7  7  7  7  7  7  7  7  7
7  7  7  8  8  8  8  8  8
8  8  8  8  8  8  9  9  9
9  9  9  9  9  9  9  9  9
10 10 10 10 10 10 10 10 10
10 10 11 11 11 11 11 11 11
11 11 11 11 11 12 12 12 12
12 12 12 12 12 12 12 12 13
13 13 13 13 13 13 13 13 13
13 14 14 14 14 14 14 14 14
14 14 14 14 15 15 15 15 15
 
{ 0 1 2 3 4 5 6 7 8 9 10 11 12 }
{ 13 14 15 16 17 18 19 20 21 22 23 24 25 }
{ 26 27 28 29 30 31 32 33 34 35 36 37 38 }
{ 39 40 41 42 43 44 45 46 47 48 49 50 51 }
{ 52 53 54 55 56 57 58 59 60 61 62 63 64 }
{ 65 66 67 68 69 70 71 72 73 74 75 76 77 }
{ 78 79 80 81 82 83 84 85 86 87 88 89 90 }
{ 91 92 93 94 95 96 97 98 99 100 101 102 103 }
{ 104 105 106 107 108 109 110 111 112 113 114 115 116 }
{ 117 118 119 120 121 122 123 124 125 126 127 128 129 }
{ 130 131 132 133 134 135 136 137 138 139 140 141 142 }
{ 143 144 145 146 147 148 149 150 151 152 153 154 155 }
{ 156 157 158 159 160 161 162 163 164 165 166 167 168 }
{ 169 170 171 172 173 174 175 176 177 178 179 180 181 }
{ 182 183 184 185 186 187 188 189 190 191 192 193 194 }
{ 195 196 197 198 199 }
 
 
Cyclic
1  2  0  1  2  0  1  2  0 
4  5  3  4  5  3  4  5  3 
7  8  6  7  8  6  7  8  6 
10 11  9 10 11  9 10 11  9 
13 14 12 13 14 12 13 14 12 
1  2  0  1  2  0  1  2  0
4  5  3  4  5  3  4  5  3
7  8  6  7  8  6  7  8  6
10 11  9 10 11  9 10 11  9 
13 14 12 13 14 12 13 14 12 
1  2  0  1  2  0  1  2  0 
4  5  3  4  5  3  4  5  3 
7  8  6  7  8  6  7  8  6 
10 11  9 10 11  9 10 11  9 
13 14 12 13 14 12 13 14 12 
1  2  0  1  2  0  1  2  0 
4  5  3  4  5  3  4  5  3 
7  8  6  7  8  6  7  8  6 
10 11  9 10 11  9 10 11  9 
13 14 12 13 14 12 13 14 12 
 
{ 0 3 6 9 50 53 56 59 100 103 106 109 150 153 156 159 }
{ 1 4 7 51 54 57 101 104 107 151 154 157 }
{ 2 5 8 52 55 58 102 105 108 152 155 158 }
{ 10 13 16 19 60 63 66 69 110 113 116 119 160 163 166 169 }
{ 11 14 17 61 64 67 111 114 117 161 164 167 }
{ 12 15 18 62 65 68 112 115 118 162 165 168 }
{ 20 23 26 29 70 73 76 79 120 123 126 129 170 173 176 179 }
{ 21 24 27 71 74 77 121 124 127 171 174 177 }
{ 22 25 28 72 75 78 122 125 128 172 175 178 }
{ 30 33 36 39 80 83 86 89 130 133 136 139 180 183 186 189 }
{ 31 34 37 81 84 87 131 134 137 181 184 187 }
{ 32 35 38 82 85 88 132 135 138 182 185 188 }
{ 40 43 46 49 90 93 96 99 140 143 146 149 190 193 196 199 }
{ 41 44 47 91 94 97 141 144 147 191 194 197 }
{ 42 45 48 92 95 98 142 145 148 192 195 198 }
{ }
 
 
Hash
8  2 12  9  7  4  9 13 15 
14 10 13 14 15  9  7  1  5 
1 13  1 11  1  8 13  6  2 
6 13 12 14 12 11  2  9  3 
5 11 11 14  2 12  2  4  8 
9  1 14 13 15  4  1  6  1 
12  4  6 12  1 13  1  1 10 
7 14  5  2  7 13  4  8  9 
13  9  9 12  7  4  2 14  8 
8 11 11 14  9  0  2  0  4 
9  0  3  3 10  4 12  3  8 
9  6  9  7  7 11 11 14 10 
12 13 13 15 11 11 14  7  8 
13  4 13 14 11  9  3  5 14 
11 13  6  8 14 12  0  0  5 
7  9  9  9  0 10 10  8  5 
1 11 12 12 12 10  3  6  7 
2  6  1 10  2  4  1  5  1 
10  8  0 10  2 15 13 12  1 
8 14 15  8 14  4  5  1  6 
    
{ 96 98 102 147 148 155 183 }
{ 18 21 23 25 52 57 59 65 67 68 161 173 177 179 189 198 }
{ 2 29 30 37 45 47 74 87 97 110 171 175 185 }
{ 39 103 104 108 120 137 167 }
{ 6 10 48 56 62 77 80 86 99 106 132 176 196 }
{ 19 41 73 138 149 159 178 190 197 }
{ 28 31 58 63 112 143 150 160 168 172 199 }
{ 5 17 71 75 85 114 115 128 151 169 }
{ 0 1 26 40 49 70 78 89 91 109 129 144 158 182 191 194 }
{ 4 7 16 38 51 79 82 83 95 101 111 113 136 140 152 153 154 }
{ 12 69 105 119 156 157 166 174 181 184 }
{ 20 24 36 42 43 50 92 93 116 117 125 126 130 135 141 162 }
{ 3 33 35 46 61 64 84 107 121 146 163 164 165 180 188 }
{ 8 13 22 27 32 54 66 76 81 122 123 131 133 142 187 }
{ 11 14 34 44 53 60 72 88 94 100 118 127 134 139 145 192 195 }
{ 9 15 55 90 124 170 186 193 }

Construct Shape Object

TiledArray supports two types of arrays: dense and sparse. If you are using dense arrays then you do not need to provide a shape object when constructing your arrays. However, to use block-sparse arrays you must use the sparse variant of the TA::DistArray class; you will also need to provide a TA::SparseShape object to its constructor. Note: although it is possible to use user-defined Shape classes, here we only discuss the stadnard TA::SparseShape class provided as a standard component of TiledArray.

A TA::SparseShape can be thought of as a dense (local) array whose elements are the Frobenius norm values for each tile. Hence the extents of the shape object are simply the extents of the tile range of the TiledRange object. Frobenius norm is chosen since its submultiplicative character makes it possible to bound the norms of tensor products; this is essential to be able to predict the shape of the result of a tensor expression.

There are two methods for constructing shape objects: distributed and replicated. You want to use distributed construction when computation of shape norms is expensive. When using distributed construction, contributions to the shape are reduced over all processes (via an all-reduce algorithm). Conversely, you want to use replicated construction when computing tile norms is inexpensive and takes less time than sharing the shape data.

The steps required to initialize a sparse shape are:

Set the zero tile threshold
Construct a [TiledRange](TiledRange) object
Construct a [process map](Construct a process map) (optional)

Zero-Tile Threshold

The zero-tile threshold is used to determine whether a tile zero or non-zero. A tile is considered to be zero if the 2-norm of the tile divided by the number of elements in the tile is less than the given threshold. That is:

tile.norm() / tile.range().volume() < TA::SparseShape::threshold()

To set the zero-tile threshold call:

TA::SparseShape::threshold(my_threshold);

where my_threshold is the zero threshold you specify for your application. This threshold is a global value and is used for all SparseShape objects. Because the zero-tile threshold is shared by all shapes, it is recommended that you set this value only once at the beginning of your program. If you change the threshold during the execution of your application, it affect all subsequent zero-tile checks but it will not change shape data. You are responsible for ensuring that changes the the threshold value during execution do not adversely affect your application.

Distributed SparseShape Construction

With distributed SparseShape construction, the shape data is partially initialized in each process. With this method, only set tile norms for local tiles, otherwise the norm data stored in shape will be artificially inflated.

The advantage of this method is that computation of tile norms is distributed among all processes, but requires communication between processes. Distributed construction is preferred when the cost of recomputing tile norms on all processes is too high or impractical. The tile norms are shared among processes by the TA::SparseShape constructor via an all-reduce summation.

With distributed construction, it is convenient to use a process map to help partition the work load. The process map can then be used to construct TA::DistArray objects.

// User provided tile factory function.
Tensor<double> make_tile(const TA::Range& range);
 
// ...
 
// tile norms are provided as a dense tensor of floats
TA::Tensor<float> tile_norms(trange.tile_range());
for(std::size_t i = 0; i < tile_norms.volume(); ++i) {
  if(pmap->is_local(i)) {
    Tensor<double> tile = make_tile(trange.make_tile_range(i));
 
    tile_norm[i] = tile.norm();
  
    // ...
 
  } else {
    tile_norms[i] = 0;
  }
}

Then construct the TA::SparseShape object with the tile norm and tiled range.

TA::SparseShape<float> shape(world, tile_norms, trange);

Note that in the above example we loop over every possible local tile and compute it's norm. For mostly sparse arrays it is necessary to loop over the nonzero tiles only. The following example demonstrates how to do this for a matrix with nonzero blocks on the diagonal only.

// tile norms will be provided as a sequence of nonzero elements
std::vector<std::pair<std::array<size_t,2>,float>> tile_norms;
// n = the number of tiles in each dimension of the matrix
for(std::size_t i = 0; i < n; ++i) {
  const auto ii = i * n + i;  // the tile ordinal index
  if(pmap->is_local(ii)) {
    // compute_tile_norm({i,i}) returns the norm estimate of tile {i,i}
    tile_norm.push_back(std::make_pair(std::array<size_t,2>{i,i},compute_tile_norm({i,i})));
  }
}
TA::SparseShape<float> shape(world, tile_norms, trange);

Replicated SparseShape Construction

With replicated SparseShape construction, the shape data is fully initialized in all processes. It is important that the shape data be identical on all processes, otherwise your application will not function correctly (most likely it will deadlock).

The advantage of this method is that it does not require communication between process, but computation of tile norms for all tiles must be done on all nodes. This method is preferred when the cost of recomputation of tile norms is less than cost of communication used in distributed shape construction.

First, create a TA::Tensor<float> object that contains the 2-norm (or Frobenius Norm) of each tile.

// User provided tile factory function.
Tensor<double> make_tile(const TA::Range& range);
 
// ...
 
TA::Tensor<float> tile_norms(trange.tiles_range());
for(std::size_t i = 0; i < tile_norms.volume(); ++i) {
  Tensor<double> tile = make_tile(trange.make_tile_range(i));
 
  tile_norm[i] = tile.norm();
  
  // ...
}

Then construct the TA::SparseShape object with the tile norm and tiled range.

TA::SparseShape<float> shape(tile_norms, trange);

Construct a DistArray

Once you have a TiledRange and optionally shape and process map constructed, you are ready to construct a DistArray object. TA::DistArray class is parametrized by 2 types:

Tile – an Array type used to represent tiles of the DistArray object.
Policy – a policy type that configures the behavior of DistArray; this includes whether DistArray is dense or block-sparse, which Range and TiledRange types are used, etc.

The ability to parametrize TA::DistArray is essential for many advanced applications: for example, the ability to customize tiles makes it possible to compute with arrays whose tiles are generated lazily (on-the-fly), support computing on heterogeneous platforms and/or with disk/NVRAM-based tile storage, utilize compressed tile formats, use multiprecision representations, etc. Similarly, by customizing Policy it is possible to implement more general sparsity types than illustrated in this guide. However, user-defined Tiles and Policies is a more advanced topic that will be covered elsewhere; here we will focus on the two most common cases that are supported out-of-the-box: dense and block-sparse DistArray with dense CPU-only tiles over integers, reals, and complex numbers. To make using such DistArrays easier TiledArray defines the following type aliases:

TA::TArray<Ring>: dense DistArray over ring type Ring (alias for TA::DistArray<TA::Tensor<Ring>,TA::DensePolicy>)
TA::TArrayD: dense DistArray over double (alias for TA::TArray<double>)
TA::TArrayF: dense DistArray over float
TA::TArrayZ: dense DistArray over std::complex<double>
TA::TArrayC: dense DistArray over std::complex<float>
TA::TArrayI: dense DistArray over int
TA::TArrayL: dense DistArray over long
TA::TSpArray<Ring>: block-sparse DistArray over ring type Ring (alias for TA::DistArray<TA::Tensor<Ring>,TA::SparsePolicy>)
TA::TSpArrayD: block-sparse DistArray over double (alias for TA::TSpArray<double>)
TA::TSpArrayF: block-sparse DistArray over float
TA::TSpArrayZ: block-sparse DistArray over std::complex<double>
TA::TSpArrayC: block-sparse DistArray over std::complex<float>
TA::TSpArrayI: block-sparse DistArray over int
TA::TSpArrayL: block-sparse DistArray over long

Throughout the rest of the guide we will use these aliases instead of using more verbose TA::DistArray type (note, however, that when debugging your code that uses these aliases most debuggers will show the name of the full type rather than the alias names).

This example demonstrates how to construct dense and sparse DistArrays:

// Construct a dense DistArray (of doubles) with the default process map
TA::TArrayD a1(world, trange);
 
// Construct a dense DistArray with a user specified process map
TA::TArrayD a2(world, trange, pmap);
 
// Construct a sparse DistArray with the default process map
TA::TSpArrayD a3(world, trange, shape);
 
// Construct a sparse DistArray with a user specified process map
TA::TSpArrayD a4(world, trange, shape, pmap);

Recall that DistArray objects have their data distributed across the entire World in which they are constructed. To ensure a consistent state their constructor is a collective operation, i.e. it must be invoked on every processor with the same arguments.

Initializing Tiles

There are several methods available to initialize array tiles. Users can initialize tiles by calling a Array::set with index and

a tile object,
a future to a tile object,
an iterator tile data, or
a constant to fill the tile. The preferred method is to construct tiles via MADNESS tasks and provide a madness::Future for the tile (see example below).

Explicit Tile Initialization

The easiest method to initialize a DistArray is to loop over local tiles and explicitly initialize each tile. This method distributes initialization work over all processes in the World. Here's the example:

// Construct a dense array
TA::TArrayD array(world...);
// Initialize local tiles
for(TArrayD::iterator it = array.begin(); it != array.end(); ++it) {
  // Construct a tile
  TArrayD::value_type tile(array.trange().make_tile_range(it.index()));
 
  // Fill tile with data
  for(std::size_t i = 0; i < tile.size(); ++i)
    tile[i] = 0.0;
 
  // Insert the tile into the array
  *it = tile;
}

The outer loop in this example iterates over the local tiles of array. Within the loop body we first create an tile (an object of TArrayD::value_type type, which in this case is TA::Tensor<double>). Then we loop over its elements and assign each to zero.

N.B. Of course, filling a DistArray with a constant is such a common use case that there's already a method for exactly that: array.fill(0.0).

There are more serious issues with the last example. First, it is too verbose. Second, it's not generic enough (i.e. trying to reuse it for a sparse DistArray would require changing a few lines). Both issues can be solved by using modern C++ features:

// Initialize local tiles
for(auto it = begin(array); it != end(array); ++it) {
  // Construct a tile
  auto tile = decltype(array)::value_type(array.trange().make_tile_range(it.index()));
 
  // Fill tile with data
  std::fill(tile.begin(), tile.end(), 0.0);
 
  // Insert the tile into the array
  *it = tile;
}

The new code is better in a few ways:

explicit use of array's type is eliminated thanks to auto and decltype (caveat: type deduction can make it more difficult to diagnose compilation errors or introduce unwanted conversions), and
the inner loop has been replaced by a more efficient and cleaner std::fill (N.B. any modern compiler at the max optimization level will replace std::fill with call to memset when appropriate, so this is the fastest way to fill the tile).

You can also initialize tile elements using a coordinate index instead of an ordinal index. The following example is equivalent to the previous example, except the tile elements are accessed via a coordinate index.

// Add local tiles
for(auto it = begin(array); it != end(array); ++it) {
  // Construct a tile
  auto tile = decltype(array)::value_type(array.trange().make_tile_range(it.index()));
 
  // Store a reference to the start and finish array of the tile
  const auto& lobound = tile.range().lobound();
  const auto& upbound = tile.range().upbound();
 
  // Fill tile with data
  // this explicitly assumes order-4 tensors!
  std::size_t i[] = {0,0,0,0};  // instead of fundamental array could use std::array, std::vector, or any SequenceContainer
  for(i[0] = lobound[0]; i[0] != upbound[0]; ++i[0])
    for(i[1] = lobound[1]; i[1] != upbound[1]; ++i[1])
      for(i[2] = lobound[2]; i[2] != upbound[2]; ++i[2])
        for(i[3] = lobound[3]; i[3] != upbound[3]; ++i[3])
          tile[i] = 0.0;
 
  // Insert the tile into the array
  *it = tile;
}

Note that in the examples shown so far tile initialization is parallelized over MPI processes only; on each process only the main thread does the initialization work. To parallelize over threads on each process we can also initialize tiles by submitting within MADNESS tasks. To do this we need to define a task function that will generate tiles. For example:

auto make_tile(const TA::Range& range) {
  // Construct a tile
  TA::TArrayD::value_type tile(range);
 
  // Fill tile with data
  std::fill(tile.begin(), tile.end(), 0.0);
 
  return tile;
}

Using make_tile(), the first example can be rewritten to generate tiles in parallel.

// Add local tiles
for(auto it = begin(array); it != end(array); ++it) {
  // Construct a tile using a MADNESS task.
  auto tile = world.taskq.add(& make_tile, array.trange().make_tile_range(it.index()));
 
  // Insert the tile into the array
  *it = tile;
}

Pushing off the initialization work to MADNESS tasks makes initialization asynchronous, i.e. actual initialization work will happen after task creation. However, in general there is no need to wait for the initialization work to complete: it is completely safe to use array in TiledArray expressions even though its initialization may not be complete yet. DistArray was designed for such asynchronous execution from the ground up.

Optimized Tile Initialization

In the above example, we generated one task per tile. However, there is a small overhead associated with generating and running a task. If the tiles are very small and/or the time required to initialize a tile is very small, then the overhead from creating and running tasks may cause your application to run slower in parallel than serially. To alleviate this problem we need to create tasks that initialize several tiles at once.

The example below, does this by recursively dividing an iterator range in half until the number of elements in the range is less than or equal to block_size. Once the size of the iterator range is small enough, the task will initialize the tiles in the iterator subrange. You do not want to make block size too small or too big, but it is usually fairly easy to achieve optimal performance.

// Construct a tile filled with zeros
template <typename Iterator>
void make_tile(
    TA::TArrayD& array,
    Iterator first,
    Iterator last,
    const std::size_t block_size)
{
  //Make tasks that generate more than one tile.
  std::size_t size = std::distance(first, last);
  while(size > block_size) {
    // Divide the iterator range in half, middle = (last - first)/2
    Iterator middle = first;
    size /= 2;
    std::advance(middle, size);
 
    // Construct a task to evaluate middle to last
    make_tile_task(array, middle, last, block_size);
 
    // This task will now evaluate first to middle
    last = middle;
  }// This loop uses tasks to generates tasks.
  // once the size is small enough then use the current task to assign tiles.
 
  // Assign portion of array
  for(; first != last; ++first) {
 
    // Construct tile
    auto tile = TA::TArrayD::value_type(array.trange().make_tile_range(first.index()));
 
    // Fill tile with your data, here it is 0's
    std::fill(tile.begin(), tile.end(), 0.0);
 
    // Add the tile to the array
    *first = tile;
  }
}
 
template <typename Iterator>
void make_tile_task(TA::TArrayD &array, Iterator first, Iterator last, const std::size_t block_size){
  //Generate a madness task to make tile.  This assumes you defined the trange for array elsewhere.
  array.world().taskq.add(& make_tile<Iterator>, array, first, last, block_size);
}
 
void make_array(TA::TArrayD &array, std::size_t block_size) {
  make_tile_task(array, begin(array), end(array), block_size);
}

make_array is the top-level function that initializes an array:

make_array(array, 2); // each task will initialize up to 2 tiles

Complete Example Program

This example shows a complete program that constructs arrays in parallel and performs a tensor contraction.

#include <tiledarray.h>
 
// Construct a TA::Tensor<T> filled with v
template <typename T>
TA::Tensor<T> make_tile(const TA::Range& range, const double v) {
  // Allocate a tile
  TA::Tensor<T> tile(range);
  std::fill(tile.begin(), tile.end(), v);
 
  return tile;
}
 
// Fill array x with value v
void init_array(TA::TArrayD& x, const double v) {
  // Add local tiles to a
  for(auto it = begin(x); it != end(x); ++it) {
    // Construct a tile using a MADNESS task.
    auto tile = x.world().taskq.add(make_tile<double>, x.trange().make_tile_range(it.index()), v);
 
    // Insert the tile into the array
    *it = tile;
  }
}
 
int main(int argc, char* argv[]) {
  // Initialize runtime
  auto& world = TA::initialize(argc, argv);
 
  // Construct tile boundary vector
  std::vector<std::size_t> tile_boundaries;
  for(std::size_t i = 0; i <= 16; i += 4)
    tile_boundaries.push_back(i);
 
  // Construct a set of TiledRange1's
  std::vector<TA::TiledRange1>
    ranges(2, TA::TiledRange1(tile_boundaries.begin(), tile_boundaries.end()));
 
  // Construct the 2D TiledRange
  TA::TiledRange trange(ranges.begin(), ranges.end());
 
  // Construct array objects.
  TA::TArrayD a(world, trange);
  TA::TArrayD b(world, trange);
  TA::TArrayD c(world, trange);
 
  // Initialize a and b.
  init_array(a, 3.0);
  init_array(b, 2.0);
 
  // Print the content of input tensors, a and b.
  std::cout << "a = \n" << a << "\n";
  std::cout << "b = \n" << b << "\n";
 
  // Compute the contraction c(m,n) = sum_k a(m,k) * b(k,n)
  c("m,n") = a("m,k") * b("k,n");
 
  // Print the result tensor, c.
  std::cout << "c = \n" << c << "\n";
 
  TA::finalize();
  return 0;
}

Note that the tasks that initialize a and b will execute during and after the corresponding init_array statements; in fact initialization of a and b can overlap.. If your initialization work needs to be performed in particular sequence you may need to add world.gop.fence() to ensure that all preceding work in the particular world has finished.

Constructing Replicated Arrays

There are two methods for generating replicated Arrays. The first method distributes computation, where data for each tile is generated on one node and distributed to all other nodes. The communication cost for this method is O(n(n-1)). This type of construction is appropriate when the data is small but expensive to compute.

The second method is replicated computation, where the data for each tile is generated on all nodes. Since the data is generated on all nodes, there is no communication with this method. Replicated computation is appropriate for data that is inexpensive to compute and/or the communcation cost in the first method is greater than the computation time.

If you want to use a hybrid approach, where each tile is computed on a small subset of nodes and distributed to the remaining, you should construct a replicated Array and write your own algorithm to computing and distributing data.

Distributed Computation

The procedure for constructing a replicated array with distributed computation is the same as constructing other replicated arrays, except Array::make_replicated() is called after the local tiles have been inserted into the array.

// Construct a distributed array.
TA::TArrayD array(world, trange);
 
// Add local tiles
for(auto it = begin(array); it != end(array); ++it) {
  // Construct a tile using a MADNESS task.
  auto tile =
    world.taskq.add(& make_tile, array.trange().make_tile_range(it.index()));
 
  // Insert the tile into the array
  array.set(it.index(), tile);
}
 
// Convert the distributed array to a replicated array,
// add distribute data.
array.make_replicated();

Replicated Computation

The procedure for constructing a replicated array with replicated computation is similar to the distributed computation method, except the array is constructed with a replicated process map (pmap).

// Construct a replicated array.
auto replicated_pmap = std::make_shared<TA::detail::ReplicatedPmap>(world, trange.tiles_range().volume());
TA::TArrayD array(world, trange, replicated_pmap);
 
// Add all tiles
for(std::size_t i = 0; i < array.size(); ++i) {
  // Construct a tile using a MADNESS task.
  auto tile =
    world.taskq.add(& make_tile, array.trange().make_tile_range(i));
 
  // Insert the tile into the array
  array.set(i, tile);
}

Tensor Expressions

Examples of tensor expressions:

E("i,j") = 2.0 * A("i,k") * B("k,j") + C("k,j") * D("k,i");
 
C("i,j") = A("i,j") + B("i,j");
 
B("i,j") = -A("i,j");
 
C("i,j") = multiply(A("i,j"), B("i,j"));
 
double x = A("i,j").dot(B("j,i"));
 
double n = A("i,j").norm2();